Prologue
When training a neural network, our goal is to find parameters $\hat{W} = \{W_l\}_{1 \leq l \leq L}$ that minimize a loss function $L(\hat{W})$ with respect to some training data. This loss function is typically non-convex and/or intractable to compute exactly. Thus, we resort to iterative optimization algorithms to find a decent local minimum instead.
And every minute choice we make on how we approximate $L$ leads to a different optimization algorithm. To illustrate this simply, let’s focus on one of the parameters $W_l$ and let’s take the Taylor expansion of $L$ around $W_l$:
$$L(W_l + \Delta W_l) = L(W_l) + \langle\nabla L(W_l), \Delta W_l\rangle_F + \frac{1}{2} \langle\Delta W_l, H(W_l) \Delta W_l\rangle_F + \ldots,$$where $\nabla L(W_l)$ is the gradient of $L$ at $W_l$, $H(W_l)$ is the Hessian of $L$ at $W_l$, and $\langle\cdot, \cdot\rangle_F$ is the Frobenius inner product:
$$\langle A, B\rangle_F = \text{tr}(A^T B) = \sum_{i,j} A_{ij}B_{ij}.$$Our goal at each iteration then is to find $\Delta W_l$ that minimizes $L(W_l + \Delta W_l)$. I.e.:
$$\Delta W_l^* = \arg\min_{\Delta W_l} L(W_l + \Delta W_l)$$And from here, we have three choies on how to approximate $L$ (and consequently $\Delta W_l^*$):
Second-order methods. Drop the third-order and subsequent terms in the Taylor expansion:
$$\Delta W_l^* = \arg\min_{\Delta W_l} \{\langle\nabla L(W_l), \Delta W_l\rangle_F + \frac{1}{2} \langle\Delta W_l, H(W_l) \Delta W_l\rangle_F\}$$Then, using Newton’s method, we get:
$$\Delta W_l^* = -H(W_l)^{-1} \nabla L(W_l)$$However, computing the Hessian, let alone inverting it, is computationally expensive. Thus, second-order optimizers like Shampoo and CASPR resort to adding more assumptions to the structure of the Hessian to get the job done. We will discuss more on this in a future post.
First-order with a soft norm penalty. Here, we approximate the second-order and subsequent terms in the Taylor expansion with a (squared-) norm penalty:
$$\Delta W_l^* = \arg\min_{\Delta W_l} \{\langle\nabla L(W_l), \Delta W_l\rangle_F + \frac{\lambda}{2} \|\Delta W_l\|^2\},$$for some norm $\|\cdot\|$ and some sharpness parameter $\lambda$ chosen a priori. This leads to the work of Bernstein & Newhouse (2024) on Steepest Descent Under Operator Norms where they show that the optimal $\Delta W_l^*$ is:
$$\Delta W_l^* = -\frac{\|\nabla L(W_l)\|^{\dagger}}{\lambda}\text{dualizer}_{\|\cdot\|}(\nabla L(W_l)),$$where $\|\cdot\|^{\dagger}$ is the dual norm of $\|\cdot\|$ and
$$\text{dualizer}_{\|\cdot\|}(X) = \arg\max_{\|T\| = 1}\langle X, T \rangle_F.$$First-order with a hard norm constraint. This is similar to the previous choice but we require that $\Delta W_l$ be of some fixed “length” $r$ with respect to the norm $\|\cdot\|$:
$$\Delta W_l^* = \arg\min_{\Delta W_l} \langle\nabla L(W_l), \Delta W_l\rangle_F \quad \text{s.t.} \quad \|\Delta W_l\| = r.$$This leads to the work of Pethick et al. (2025) on Linear Minimization Oracle (LMO) over a norm ball.
Now, notice that for $r = 1$, the only difference between the second and third choices is actually the scaling factor or the “learning rate”, the schedule of which we can tune separately. Either way, the crucial part is how we choose the norm $\|\cdot\|$–if we pick a different norm, we get a different class of optimizers.
Steepest Descent Under Operator Norms
Previous work by Bernstein & Newhouse (2024) and Pethick et al. (2025) have already worked out the dualizers for different operator norms and how they give rise to different optimizers.
Frobenius Norm $\|\cdot\|_F$: The dual norm of the Frobenius norm is the Frobenius norm itself. And its dualizer is fairly simple:
$$ \begin{align*} \|\nabla L(W_l)\|_F^{\dagger} &= \|\nabla L(W_l)\|_F\\ \text{dualizer}_{\|\cdot\|_F}(\nabla L(W_l)) &= \frac{\nabla L(W_l)}{\|\nabla L(W_l)\|_F} \end{align*} $$Thus, the update rule for steepest descent under the Frobenius norm is:
$$ \begin{align*} \Delta W_l^* &= -\frac{\|\nabla L(W_l)\|_F}{\lambda} \frac{\nabla L(W_l)}{\|\nabla L(W_l)\|_F}\\ \Delta W_l^* &= -\frac{1}{\lambda} \nabla L(W_l) \end{align*} $$which is just the update rule for Stochastic Gradient Descent (SGD).
Max-of-Max Norm $\|\cdot\|_{1 \to \infty}$: A unit-length matrix under this norm is a matrix where all entries are $\pm 1$. And we can show that the unit-length matrix $T$ that maximizes the Frobenius inner product with the gradient $\nabla L(W_l)$ is the matrix whose entries are the signs of the entries of $\nabla L(W_l)$:
$$\text{dualizer}_{\|\cdot\|_{1 \to \infty}}(\nabla L(W_l)) = \text{sign}(\nabla L(W_l))$$Thus, the update rule for steepest descent under the max-of-max norm is:
$$ \begin{align*} \Delta W_l^* &= -\frac{\|\nabla L(W_l)\|_{1 \to \infty}^\dagger}{\lambda} \text{sign}(\nabla L(W_l))\\ \Delta W_l^* &= -\frac{1}{\hat{\lambda}} \frac{\nabla L(W_l)}{\sqrt{\nabla L(W_l) \odot \nabla L(W_l)}} \end{align*} $$where $\hat{\lambda} = \frac{\lambda}{\|\nabla L(W_l)\|_{1 \to \infty}^\dagger}$ and $\odot$ is the element-wise (Hadamard) product. Note that this is the update rule for Adam without accumulation.
Spectral Norm $\|\cdot\|_{2 \to 2}$: A unit-length matrix under this norm is a matrix whose singular values are all 1. And we can show that the unit-length matrix $T$ that maximizes the Frobenius inner product with the gradient $\nabla L(W_l)$ is the matrix whose singular vectors are also the singular vectors of $\nabla L(W_l)$. We will prove this more rigorously in the next section. But for now, the dualizer for the spectral norm is:
$$\text{dualizer}_{\|\cdot\|_{2 \to 2}}(\nabla L(W_l)) = UV^T,$$where $\nabla L(W_l) = U\Sigma V^T$ is the singular value decomposition of $\nabla L(W_l)$. Thus, the update rule for steepest descent under the spectral norm is:
$$ \begin{align*} \Delta W_l^* &= -\frac{\|\nabla L(W_l)\|_{2 \to 2}^{\dagger}}{\lambda} UV^T\\ \Delta W_l^* &= -\frac{1}{\hat{\lambda}} UV^T \end{align*} $$where $\hat{\lambda} = \frac{\lambda}{\|\nabla L(W_l)\|^{\dagger}_{2 \to 2}}$ which is just the update rule for Muon.
Steepest Descent Under Schatten-$p$ Norms
We can generalize the above to the Schatten-$p$ norms.
Schatten-$p$ Norms
Definition 1: Schatten-$p$ Norm. The Schatten-$p$ norm of a matrix $A$ is defined as:
$$\|A\|_p = \left(\sum_{i=1}^{\min(m, n)} |\sigma_i(A)|^p\right)^{1/p},$$where $\sigma_i(A)$ are the singular values of $A$.
In a sense, you can think of the Schatten-$p$ norm of $A$ as the $p$-norm of the singular values of $A.$
Examples:
- $p = 1$: The Nuclear norm, $\|A\|_{S_1} = \sum_{i=1}^{\min(m,n)} |\sigma_i(A)|$
- $p = 2$: The Frobenius norm, $\|A\|_{S_2} = \left(\sum_{i=1}^{\min(m,n)} |\sigma_i(A)|^2\right)^{\frac{1}{2}} = \|A\|_F$
- $p = \infty$: The Spectral norm, $\|A\|_{S_{\infty}} = \max_{i} \sigma_i(A) = \|A\|_{2 \to 2}$
$(2)$ may be non-obvious to some, but here’s a short proof:
$$ \begin{align*} \|A\|_F &= \sqrt{\sum_{ij} A_{ij}^2} = \sqrt{tr(A^TA)} = \sqrt{tr((U\Sigma V^T)^T(U\Sigma V^T))}\\ &= \sqrt{tr(V \Sigma^2 V^T)} = \left(\sum_i \sigma_i(A)^2\right)^{\frac{1}{2}} = \|A\|_{S_2} \end{align*} $$von Neumann’s Trace Inequality
And to find the dualizers for the Schatten-$p$ norms, we need the following inequality:
Theorem (von Neumann’s Trace Inequality). Let $A$ and $B$ be two matrices. Then, the following inequality holds:
$$\text{tr}(A^TB) \leq \sum_{i=1}^{\min(m,n)} \sigma_i(A) \sigma_i(B),$$where $\sigma_i(A)$ are the singular values of $A$. And equality holds if and only if $A$ and $B$ share singular vectors.
Steepest descent under Schatten-$p$ Norms
Here, we derive the dualizer for an arbitrary Schatten-$p$ norm.
Proposition 2. The dualizer for the Schatten-$p$ norm is:
$$\text{dualizer}_{\|\cdot\|_{S_p}}(X) = U \frac{\text{diag}\left(\sigma_1(X)^{q-1}, \ldots, \sigma_{\min(m,n)}(X)^{q-1}\right)}{\|X\|_{S_q}^{q-1}} V^T$$where $X = U\Sigma V^T$ is the singular value decomposition of $X$ and $\frac{1}{p} + \frac{1}{q} = 1$.
Proof: For a given $X$, let $T^*$ be:
$$ \begin{align*} T^* &= \text{dualizer}_{\|\cdot\|_{S_p}}(X)\\ T^* &= \arg\max_{\|T\|_{S_p} = 1} \langle X, T \rangle_F\\ T^* &= \arg\max_{\|T\|_{S_p} = 1} \text{tr}(X^T T) \end{align*} $$Then, from von Neumann’s Trace Inequality, we know that $T^*$ must share singular vectors with $X$ and that:
$$T^* = \arg\max_{\|T\|_{S_p} = 1} \sum_{i=1} \sigma_i(X) \sigma_i(T)$$Thus, our optimization problem reduces to
$$\max_{\{\sigma_i(T)\}} \sum_i \sigma_i(X) \sigma_i(T) \quad\text{s.t.}\quad \sum \sigma_i(T)^p = 1$$which we can solve via Lagrange multipliers. See appendix for the full proof. For now, the solution is:
$$\sigma_i(T) = \frac{\sigma_i(X)^{q-1}}{\|X\|_{S_q}^{q-1}}$$Hence,
$$T^* = \text{dualizer}_{\|\cdot\|_{S_p}}(X) = U \frac{\text{diag}\left(\sigma_1(X)^{q-1}, \ldots, \sigma_{\min(m,n)}(X)^{q-1}\right)}{\|X\|_{S_q}^{q-1}} V^T\quad\blacksquare$$
The proof that the dual norm of the Schatten-$p$ norm is the Schatten-$q$ norm where $\frac{1}{p} + \frac{1}{q} = 1$ actually follows directly from here:
Corollary 3. The dual norm of the Schatten-$p$ norm is the Schatten-$q$ norm where $\frac{1}{p} + \frac{1}{q} = 1$.
Proof: For a given $X$, we want to show that
$$\|X\|_{S_p}^{\dagger} = \|X\|_{S_q}$$From the definition of the dual norm, we have:
$$ \begin{align*} \|X\|_{S_p}^{\dagger} &= \sup_{\|T\|_{S_p} \leq 1} \langle X, T \rangle_F\\ \|X\|_{S_p}^{\dagger} &= \sup_{\|T\|_{S_p} \leq 1} \text{tr}(X^T T) \end{align*} $$Following Proposition 2, we know that we can achieve the supremum by choosing $T = \text{dualizer}_{\|\cdot\|_{S_p}}(X)$. Thus,
$$ \begin{align*} \|X\|_{S_p}^{\dagger} &= \text{tr}\left(X^T U \frac{\text{diag}\left(\sigma_1(X)^{q-1}, \ldots, \sigma_{\min(m,n)}(X)^{q-1}\right)}{\|X\|_{S_q}^{q-1}} V^T\right)\\ &= \sum_i \sigma_i(X) \frac{\sigma_i(X)^{q-1}}{\|X\|_{S_q}^{q-1}}\\ &= \frac{1}{\|X\|_{S_q}^{q-1}} \sum_i \sigma_i(X)^q\\ &= \frac{\|X\|_{S_q}^q}{\|X\|_{S_q}^{q-1}}\\ \|X\|_{S_p}^{\dagger} &= \|X\|_{S_q}\quad\blacksquare \end{align*} $$
Finally,
Theorem 4. The update rule for steepest descent under the Schatten-$p$ norm is:
$$\Delta W_l^* = -\frac{1}{\hat{\lambda}} U \frac{\text{diag}\left(\sigma_1(\nabla L(W_l))^{q-1}, \ldots, \sigma_{\min(m,n)}(\nabla L(W_l))^{q-1}\right)}{\|\nabla L(W_l)\|_{S_q}^{q-1}} V^T$$where $\hat{\lambda} = \frac{\lambda}{\|\nabla L(W_l)\|_{S_q}}$, $\nabla L(W_l) = U\Sigma V^T$ is the singular value decomposition of $\nabla L(W_l)$, and $\frac{1}{p} + \frac{1}{q} = 1$.
The proof follows directly from Proposition 2 and Corollary 3.
Sanity Checks
Our results should match prior results for $p = 2, \infty$:
For $p = 2$, the Frobenius norm: $q = 2$ and $\|\cdot\|_{S_2}^\dagger = \|\cdot\|_{S_2} = \|\cdot\|_F$. Thus,
$$ \begin{align*} \text{dualizer}_{\|\cdot\|_{S_2}}(X) &= U \frac{\text{diag}\left(\sigma_1(X)^{2-1}, \ldots, \sigma_{\min(m,n)}(X)^{2-1}\right)}{\|X\|_{S_2}^{2-1}} V^T\\ \text{dualizer}_{\|\cdot\|_F}(X) &= \frac{X}{\|X\|_F} \end{align*} $$Thus,
$$ \begin{align*} \Delta W_l^* &= -\frac{\|\nabla L(W_l)\|_F}{\lambda} \frac{\nabla L(W_l)}{\|\nabla L(W_l)\|_F}\\ \Delta W_l^* &= -\frac{1}{\lambda} \nabla L(W_l) \end{align*} $$For $p = \infty$, the Spectral norm: $q = 1$ and $\|\cdot\|_{S_\infty}^\dagger = \|\cdot\|_{S_1}$. Thus,
$$ \begin{align*} \text{dualizer}_{\|\cdot\|_{S_\infty}}(X) &= U \frac{\text{diag}\left(\sigma_1(X)^{1-1}, \ldots, \sigma_{\min(m,n)}(X)^{1-1}\right)}{\|X\|_{S_1}^{1-1}} V^T\\ \text{dualizer}_{\|\cdot\|_{2 \to 2}}(X) &= UV^T \end{align*} $$Thus,
$$ \begin{align*} \Delta W_l^* &= -\frac{\|\nabla L(W_l)\|_{S_1}}{\lambda} UV^T\\ \Delta W_l^* &= -\frac{1}{\hat{\lambda}} UV^T \end{align*} $$where $\hat{\lambda} = \frac{\lambda}{\|\nabla L(W_l)\|_{S_1}}$.
Both of which matches prior results. And as a fun exercise, try to prove that the dualizer for the Schatten-$1$ norm, or the Nuclear norm, results in a rank-$k$ matrix where $k$ is the multiplicity of the largest singular value.
What Does the Dualizer Actually Do?
We observe that steepest descent under the Schatten-$p$ norm very quickly starts to “look like” steepest descent under the Spectral norm as $p$ approaches $\infty$. This is probably why optimizers that merely approximately semi-orthogonalize the gradients like Sketching and Muon work so well in practice despite resulting in (relatively) high-variance of singular values post-dualization.
To support this, we show that the (1) variance of singular values, and the (2) relative size, and (3) stable rank of the gradients post-dualization under the Schatten-$p$ norm converge to those of the Spectral norm very quickly as $p$ approaches $\infty$. And in fact, at $p = 32$, the results are already very close to those of the Spectral norm.
On the variance of singular values
Proposition 5. The variance of the singular values post-dualization under the Schatten-$p$ Norm converges quadratically to $0$ as $p$ approaches $\infty$.
Proof: Let $t_i$ be the $i$-th singular value post-dualization. From Proposition 2 earlier, we have
$$ \begin{align*} t_i &= \left(\frac{\sigma_i(\nabla L(W_l))}{\|\nabla L(W_l)\|_{S_q}}\right)^{q-1}\\ t_i &= \exp\left((q-1)\ln\frac{\sigma_i(\nabla L(W_l))}{\|\nabla L(W_l)\|_{S_q}}\right)\\ t_i &\approx 1 + (q-1)\ln\frac{\sigma_i(\nabla L(W_l))}{\|\nabla L(W_l)\|_{S_q}} \end{align*} $$where the last line follows from first-order Taylor approximation of $t_i$. Thus, the mean and variance are:
$$ \begin{align*} \mathbb{E}[t_i] &\approx 1 + (q-1)\mathbb{E}\left[\ln\frac{\sigma_i(\nabla L(W_l))}{\|\nabla L(W_l)\|_{S_q}}\right]\\ \mathbb{E}[t_i] &\approx 1 + (q-1)\ln\frac{\mathbb{E}[\sigma_i(\nabla L(W_l))]}{\|\nabla L(W_l)\|_{S_q}}\\ t_i - \mathbb{E}[t_i] &\approx (q-1)\ln\left[\sigma_i(\nabla L(W_l)) - \mathbb{E}[\sigma_i(\nabla L(W_l))]\right]\\ Var[t_i] &\approx (q-1)^2\mathbb{E}\left[\ln^2\left[\sigma_i(\nabla L(W_l)) - \mathbb{E}[\sigma_i(\nabla L(W_l))]\right]\right]\\ Var[t_i] &\approx \frac{1}{(p-1)^2}\mathbb{E}\left[\ln^2\left[\sigma_i(\nabla L(W_l)) - \mathbb{E}[\sigma_i(\nabla L(W_l))]\right]\right] \end{align*} $$Hence, the variance of the singular values post-dualization converges quadratically to $0$ as $p$ approaches $\infty$.
Empirically, we can see this in the following plot. And at $p = 32$, the variance of the resulting singular values is already very close to $0$.

On the relative size and stable rank of gradients
Definition 6: Relative Size of a Gradient. Given a norm $\|\cdot\|$ chosen a priori, the relative size of a gradient-update $\Delta W$ relative to the parameter matrix $W$ is defined as:
$$\text{relsize}(\Delta W) = \frac{\|\Delta W\|}{\|W\|}$$
Definition 7: Stable Rank. The stable rank of a matrix $A$ is defined as
$$srank(A) = \frac{\|A\|_F^2}{\|A\|_{2 \to 2}^2}$$
As we can see in the following plot, the raw gradients have very low-stable rank. But the stable rank of the gradients post-dualization under the Schatten-$p$ norm converges very quickly to that of the Spectral norm as $p$ approaches $\infty$.

One can interpret this as, for some large enough $p$, the dualized gradient is already very close to being “maximal” in a sense. And increasing $p$ further would only offer rapidly diminishing returns.
Faster feature learning
Why do we want ‘maximal’ updates? I’d love to dive deeper into this in a future post. But for now, I’ll leave you with these:
- Weight Erasure. Because the raw gradients are naturally “small” or have low stable rank, models trained with SGD, Adam, or similar optimizers tend to get ‘stuck’ within a small region of the parameter space around the initialization (Lee et al., 2020; Jesus et al., 2021). On the other hand, optimizers like Muon that ramp up the stable rank of the gradients can quickly ’escape’ the init region and explore the parameter space more effectively. If you want to learn more about this, check out Bernstein’s blog post on weight erasure (2024).
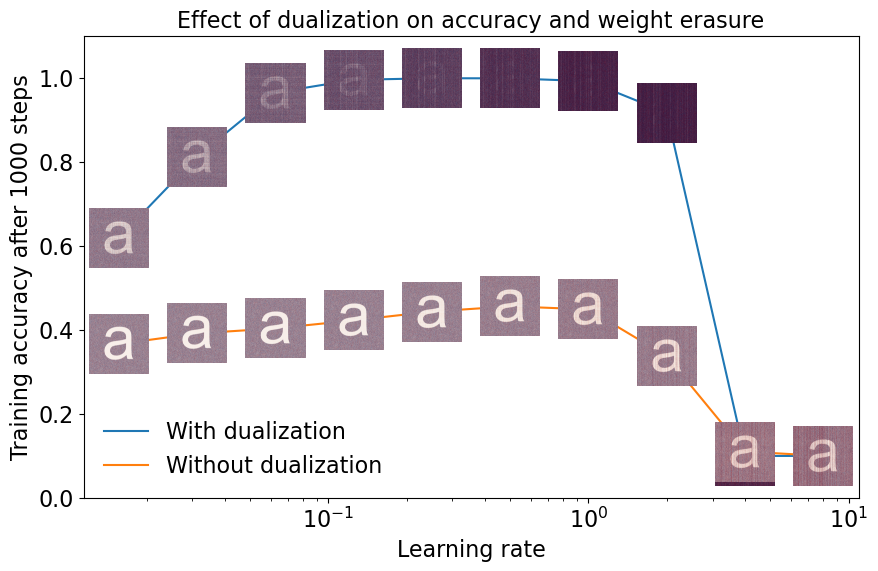
- Faster Feature Learning. Another reason we want ‘maximal’ updates is that it allows the model to learn features faster. If our updates are too small, they would vanish at larger model widths. E.g., it’s going to take you forever to learn a diverse features set on a 4096-wide model if your updates are merely rank-1. Ideally, our updates should “grow” with the model width. And, in a sense, this is what optimizers like Muon do.
That’s it for now. Until next time!
How to Cite
@misc{cesista2025schattenp,
author = {Franz Louis Cesista},
title = {{S}teepest {D}escent Under {S}chatten-p {N}orms},
year = {2025},
month = {February},
day = {7},
url = {https://leloykun.github.io/ponder/steepest-descent-schatten-p/},
}
References
- Jeremy Bernstein, Laker Newhouse (2024). Old Optimizer, New Norm: An Anthology. URL https://arxiv.org/abs/2409.20325
- Jeremy Bernstein (2024). “Weight erasure.” Available at: https://docs.modula.systems/examples/weight-erasure/
- Keller Jordan, Jeremy Bernstein, Brendan Rappazzo, @fernbear.bsky.social, Boza Vlado, Jiacheng You, Franz Cesista, Braden Koszarsky, and @Grad62304977. modded-nanogpt: Speedrunning the NanoGPT baseline. 2024. Available at: https://github.com/KellerJordan/modded-nanogpt.
- Keller Jordan, Yuchen Jin, Vlado Boza, Jiacheng You, Franz Cesista, Laker Newhouse, and Jeremy Bernstein (2024). Muon: An optimizer for hidden layers in neural networks. Available at: https://kellerjordan.github.io/posts/muon/.
- Vineet Gupta, Tomer Koren, Yoram Singer (2018). Shampoo: Preconditioned Stochastic Tensor Optimization. URL https://arxiv.org/abs/1802.09568
- Rohan Anil, Vineet Gupta, Tomer Koren, Kevin Regan, Yoram Singer (2020). Scalable second order optimization for deep learning. URL https://arxiv.org/abs/2002.09018
- Surya, S., Duvvuri, Devvrit, F., Anil, R., Hsieh, C., & Dhillon, I.S. (2024). Combining Axes Preconditioners through Kronecker Approximation for Deep Learning. International Conference on Learning Representations.
- Thomas Pethick, Wanyun Xie, Kimon Antonakopoulos, Zhenyu Zhu, Antonio Silveti-Falls, Volkan Cevher (2025). Training Deep Learning Models with Norm-Constrained LMOs. Available at: https://arxiv.org/abs/2502.07529.
- David E Carlson, Edo Collins, Ya-Ping Hsieh, Lawrence Carin, Volkan Cevher (2015). Preconditioned Spectral Descent for Deep Learning. Advances in Neural Information Processing Systems 28 (NIPS 2015)
- Lee, Jaehoon, et al. “Wide Neural Networks of Any Depth Evolve as Linear Models under Gradient Descent.” Journal of Statistical Mechanics: Theory and Experiment, vol. 2020, no. 12, Dec. 2020, p. 124002. Crossref, https://doi.org/10.1088/1742-5468/abc62b.
- Jesus, Ricardo J., et al. “Effect of Initial Configuration of Weights on Training and Function of Artificial Neural Networks.” Mathematics, vol. 9, no. 18, Sept. 2021, p. 2246. Crossref, https://doi.org/10.3390/math9182246.
- Greg Yang and James B. Simon and Jeremy Bernstein (2024). A Spectral Condition for Feature Learning. Available at: https://arxiv.org/abs/2310.17813.